Significado de «curvas de funciones trigonométricas»

1. Las seis funciones trigonométricas de un ángulo (v. Trigonometría) pueden definirse no sólo para ángulos agudos, sino para ángulos cualesquiera. La gráfica o curva cartesiana de estas funciones se obtiene expresando horizontalmente la cuantía del ángulo y en sentido vertical el correspondiente valor de la función. Las funciones del seno y coseno son utilizadas frecuentemente para representar formas ondulatorias simples (v. Periodo y periodicidad), desplazamientos armónicos sencillos y oscilaciones. Véase Coordenadas.
   
   
   La curva seno, ecuación y = sen x, es cero si x = 0 y oscila entre un valor máximo de más uno ( + 1) para x = 90° o π/2 radianes, y un valor mínimo de menos uno ( -1) para x = 270° o 3π/2 radianes. La curva se repite, para los valores positivos y negativos de x, a intervalos de 360° o 2π radianes, amplitud que constituye por eso el periodo de la función (fig. 1).
   
   
   
   
   
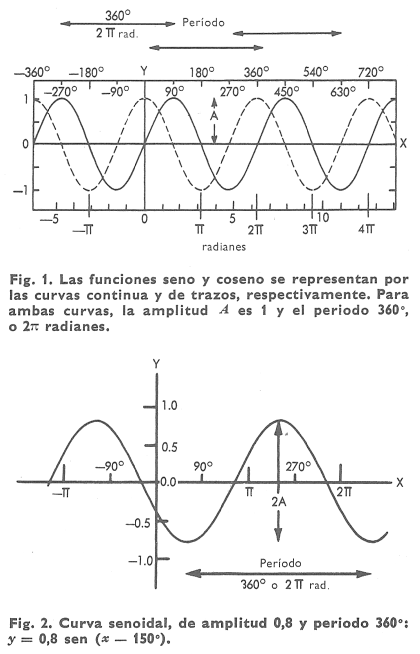
   La curva coseno, ecuación y = cos x, tiene la misma forma que la curva seno, con la cual coincidiría si se trasladara 90° (o π/2) hacia la derecha a lo largo del eje x, o sea, posee una diferencia de fase de 90° o π/2 con respecto a la curva seno; analíticamente: cos x = sen (90° - x). Ambas curvas, la del seno y la del coseno, tienen amplitud 1, que es el valor máximo absoluto de la función; además, sen x = sen (x + P) y, análogamente, cos x = cos (x + P), en donde P = 360°, que es el periodo de cada una de las funciones. Una ecuación de la forma y = A sen (x - c) es utilizada habitualmente para representar un desplazamiento armónico que se anula cuando x = c y su amplitud es A; es decir, la distancia vertical entre el máximo y el mínimo de la curva es 2A. Véase figura 2.
   
   
   La curva tangente, ecuación y = tan x, pasa por el origen de coordenadas de un lado a otro de ambos ejes y es asintótica (v. Asíntota) a las lineas verticales x = = -90° y x = +90° (fig. 3).
   
   
   
   
   
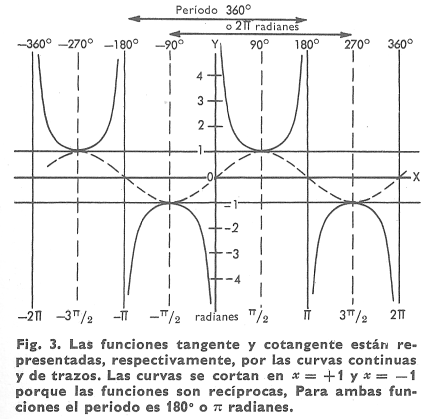
   Hay un punto de inflexión en el origen, donde la curvatura pasa de cóncava hacia abajo, a la izquierda del origen, a serlo hacia arriba, a la derecha, conservando así el lado convexo de la curva hacia el eje X. La curva se repite en otras ramas a intervalos de x de 180° o π y corta el eje X para valores de x enteros y múltiplos de π. Como la cotangente de x es la recíproca de la tangente de x, la gráfica de y = cos x es asintótica a las líneas
   
   verticales x = 0 y x = +π y corta el eje X en π/2, o 90°. Esta curva se repite también en otras ramas a intervalos de 180° y corta el eje X en los valores múltiplos enteros impares de 90°.
   
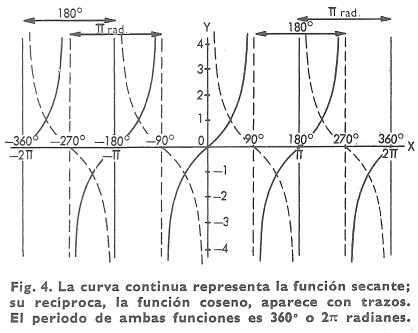
   La curva secante, ecuación y = sec x, está representada en la figura 4 junto con la curva y = cos x, su función recíproca. No existen porciones de la curva secante entre los valores +1 y -1 de y. Los valores mínimos (y = +1) de las ramas que son cóncavas ascendentes, corresponden a x = 0, ±2π, ±4π, etc.; los valores máximos (y = -1) de las ramas que son cóncavas hacia abajo corresponden a x = ±π ±3π, etcétera.
   
   
   
   
   
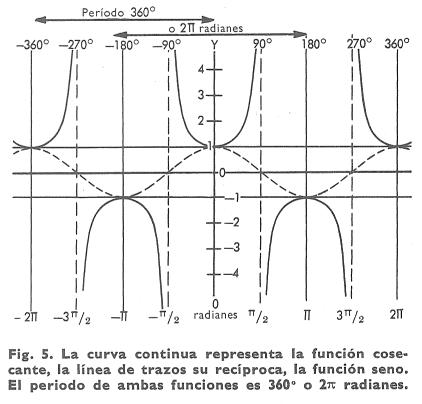
   La curva cosecante, ecuación y = cosec x, aparece en la figura 5 junto con la curva y = sen x, la función recíproca. Si las ramas de esta curva fueran desplazadas 90° hacia la izquierda coincidirían con las ramas de la curva secante.
   
   
   
   
   
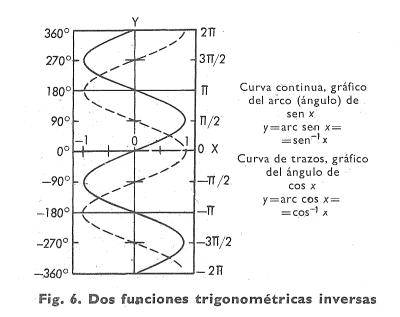
   Funciones trigonométricas inversas. La función sen -1 x, o bien, arc sen x, se conoce por la inversa de la función sen x. Su significación es «el arco cuyo seno es x». Así, y = sen -1 x;, o y = arc sen x, puede ser expresado como x = sen y. Para representar una función inversa es quizá más sencillo escribir primero la función en forma directa, como arriba (fig. 6). Véase Función.
   
   
   

Compartir

Buscar

Asistente IA

Consulta nuestro asistente de Inteligencia Artificial
¡te responderá en segundos!

Respuesta completa
Respuesta corta

[ Ayuda ] Dale información suficiente de lo que buscas, dale un contexto. El Asistente te puede dar definiciones, sinónimos y antónimos, oraciones de uso de palabras, encontrar ideas relacionadas, corregir ortografía y darte asistencia escolar sobre cualquier tema. Igualmente, te recomiendo FUERTEMENTE que uses nuestro Buscador (más abajo) para encontrar información apropiada, ya que esta fue escrita por nuestros expertos.

* ACLARACIÓN: sugerimos dejar un email para que te contactemos si vemos errores en la respuesta de la IA: leemos todas las consultas.

Esta imagen puedes emplearla con fines didácticos en la escuela, institución educativa o proyectos web.

¿Hay un error o desea enviarnos un mensaje?: enviar mensaje

No hay ningún comentario todavía