Significado de función cuadrática | Sinónimos y oraciones con ejemplos de uso de función cuadrática
Significado de «función cuadrática»
Una función cuadrática es un tipo de función matemática con ecuación f(x) = ax^2 + bx + c, donde a, b y c son constantes y a ? 0.
Se llaman cuadráticas por tener un término elevado al cuadrado.
Su gráfica es una parábola que puede abrir hacia arriba o abajo.
El vértice está en (-b/2a, f(-b/2a)) y es el punto de simetría.
Pueden tener comportamientos distintos según los valores de a, b y c, como valor mínimo o máximo.
Las raíces pueden ser reales o imaginarias según el discriminante b^2 - 4ac.
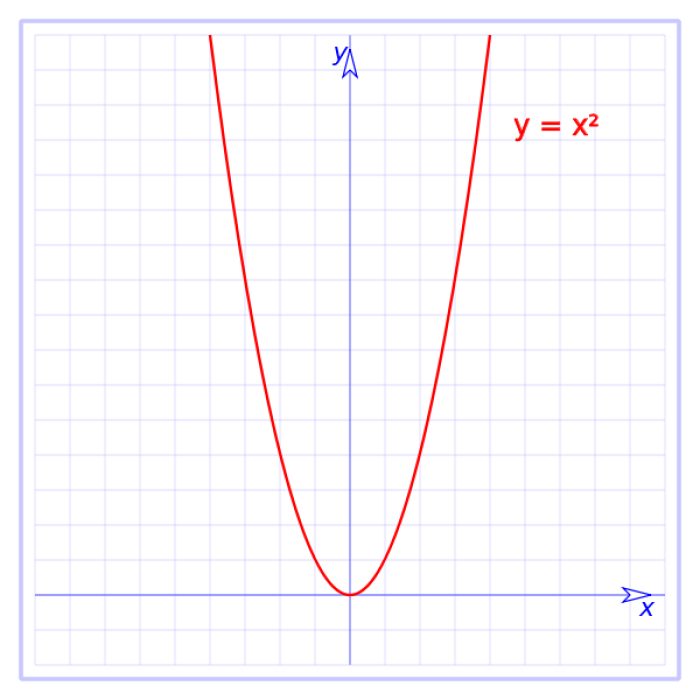
Tabla de contenido
Definición de función cuadrática
Autor: Leandro Alegsa
Número de letras: 17
Posee un total de 8 vocales: u i ó u a á i a
Y un total de 9 consonantes: f n c n c d r t c
¿Preguntas sobre el significado de esta palabra?: respondemos aquí
[ Imágenes relacionadas a "función cuadrática" ]
Esta imagen puedes emplearla con fines didácticos en la escuela, institución educativa o proyectos web.
Se llaman cuadráticas por tener un término elevado al cuadrado.
Su gráfica es una parábola que puede abrir hacia arriba o abajo.
El vértice está en (-b/2a, f(-b/2a)) y es el punto de simetría.
Pueden tener comportamientos distintos según los valores de a, b y c, como valor mínimo o máximo.
Las raíces pueden ser reales o imaginarias según el discriminante b^2 - 4ac.
- Definición de función cuadrática
- Análisis de "función cuadrática" como palabra
- Palabras cercanas a "función cuadrática"
- ¿Dudas o consultas?
Definición de función cuadrática
- Las funciones cuadráticas son un tipo de función matemática que se caracteriza por tener una ecuación de la forma f(x) = ax^2 + bx + c, donde a, b y c son constantes y a ≠ 0. Estas funciones son llamadas cuadráticas debido a que el término principal es una variable elevada al cuadrado.
Las funciones cuadráticas tienen varias propiedades y características importantes. Por ejemplo, su gráfica es una parábola, que puede abrir hacia arriba si a > 0 o hacia abajo si a < 0. El vértice de la parábola se encuentra en el punto (-b/2a, f(-b/2a)) y es el punto de simetría de la función.
Además, las funciones cuadráticas pueden tener diferentes tipos de comportamiento dependiendo de los valores de a, b y c. Por ejemplo, si a > 0, la función tiene un valor mínimo y si a < 0, tiene un valor máximo. También pueden tener raíces reales o imaginarias, dependiendo del discriminante b^2 - 4ac.
Estas funciones son ampliamente utilizadas en matemáticas y ciencias, ya que permiten modelar una variedad de fenómenos y situaciones del mundo real. Se utilizan en campos como la física, la economía, la ingeniería, entre otros.
Autor: Leandro Alegsa
← función
Diccionarios relacionados
Compartir la definición, preguntar y buscar
Compartir
Buscar
Usa la inteligencia artificial para resolver tus dudas
Fuentes bibliográficas y más información de función cuadrática:
[ Más ejemplos de oraciones y usos de "función cuadrática" ]
[ Imágenes relacionadas a "función cuadrática" ]
[ Usos en libros de "función cuadrática" ]
[ Imágenes relacionadas a "función cuadrática" ]
[ Usos en libros de "función cuadrática" ]
Análisis de función cuadrática
Cantidad de letras, vocales y consonantes de función cuadrática
Palabra inversa: acitárdauc nóicnufNúmero de letras: 17
Posee un total de 8 vocales: u i ó u a á i a
Y un total de 9 consonantes: f n c n c d r t c
¿Es aceptada "función cuadrática" en el diccionario de la RAE?
Ver si existe en el diccionario RAE: función cuadrática (RAE)Categorías donde se encuentra: función cuadrática
Matemáticas|
Palabras cercanas
|
Abreviaturas empleadas en la definición
c. = ciudad o circa
Más abreviaturas...
Más abreviaturas...
Cómo citar la definición de función cuadrática
Definiciones-de.com (2023). Definición de función cuadrática - Leandro Alegsa © 29/08/2023 url: https://www.definiciones-de.com/Definicion/de/funcion_cuadratica.php
¿Preguntas sobre el significado de esta palabra?: respondemos aquí
[ Imágenes relacionadas a "función cuadrática" ]
Esta imagen puedes emplearla con fines didácticos en la escuela, institución educativa o proyectos web.
Buscar por letra: A - B - C - D - E - F - G - H - I - J - K - L - M - N - Ñ - O - P - Q - R - S - T - U - V - W - X - Y - Z - Indice
Buscar por categoría: Anatomía - Arte y Cultura - Biología - Ciencias - Deportes - Física y química - Literatura - Matemáticas - Medicina - Palabras cultas - Religión - Zoología - más categorías
Inteligencia Artificial: Generador de oraciones
Buscar por categoría: Anatomía - Arte y Cultura - Biología - Ciencias - Deportes - Física y química - Literatura - Matemáticas - Medicina - Palabras cultas - Religión - Zoología - más categorías
Inteligencia Artificial: Generador de oraciones
|
Buscar por palabra o frase: |
NOVEDAD: ¡Síguenos en nuestras redes!
Para aprender nuevas palabras, cómo escribir mejor y cultura general.
Herramientas de análisis
Emplea lo más avanzado de IA (Inteligencia Artificial) para realizar las tareas
- Identifica la idea principal de un texto
- Resume un texto online
- Cambia un texto, para que parezca distinto
- Corrector de errores ortográficos
- Explica de manera más sencilla un texto
- Analiza la sintaxis y la semántica de una oración
- Genera oraciones con una palabra
- Cuenta la cantidad de palabras en un texto
¿Hay un error o desea enviarnos un mensaje?: enviar mensaje
Te pueden interesar
Preguntas y comentarios
No hay ningún comentario todavía