Significado de «teoría cuántica»

1. Todos los adelantos científicos de importancia que se registran en la historia de la Ciencia son virtualmente una consecuencia de su propio proceso evolutivo y tal es el caso de la Teoría Cuántica. Pocos habrán sido los avances decisivos en la Física que hayan despertado tanto interés y suscitado tan vivas controversias como la teoría enunciada por Max Planck (1858-1947), de la Universidad de Berlín, en una serie de trabajos publicados a comienzos del siglo XX. Para explicar el proceso de gestación de esta teoría es preciso describir brevemente algunos de sus antecedentes.
   
   Hacia 1881, Samuel Pierpont Langley (1834-1906) se dedicaba a estudiar, en el observatorio astronómico de Allegheny, la distribución de la energía a lo largo del espectro solar, particularmente en la región del infrarrojo. Como hasta entonces no se disponía de ningún instrumento digno de confianza para detectar la radiación infrarroja, Langley hubo de proyectar y construir el Bolómetro. Este dispositivo consiste fundamentalmente en un puente de Wheatstone, dos de cuyos brazos están constituidos por unas delgadas tiras de platino ennegrecido de unos 2 cm de largo y menos de 1 mm de ancho. Después de equilibrar el puente, se deja incidir la radiación espectral sobre una de las tiras de platino, que al absorberla se calienta, aumentando su resistencia y produciendo un desequilibrio del puente. La desviación correspondiente del galvanómetro es proporcional a la energía absorbida por la cinta de platino. Variando las partes del espectro que actúan sobre el bolómetro puede registrarse la distribución de la energía a lo largo de todo él.
   
   La invención de este aparato estimuló las investigaciones respecto a la dispersión y absorción espectrales de diversas sustancias, despertando considerable atención la emisividad de distintos radiadores, particularmente la del cuerpo negro, como función de la temperatura a la que se emite la radiación.
   
   
   
   
   
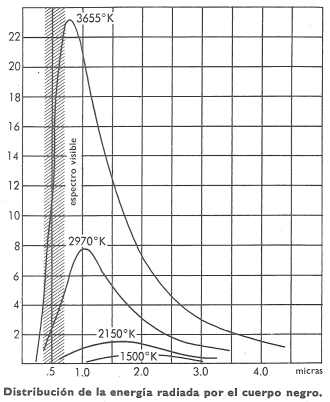
   El cuerpo negro o radiador perfecto es el que emite su radiación con intensidad mayor que cualquier otro a la misma temperatura y que absorbe totalmente cualquier radiación que incida sobre él. Aunque tal radiador ideal no existe, se le aproxima mucho en su comportamiento el cuerpo negro real que consiste en una caja, calentada eléctricamente a temperatura uniforme, en una de cuyas paredes, ennegrecidas interiormente, se ha practicado un orificio para que salga la radiación emitida. De esta radiación, dispersada mediante un espectroscopio, pueden obtenerse a distintas temperaturas las correspondientes curvas de distribución de la energía, tal como se representan en la figura 1. A la vista de esta familia de curvas, un físico se preguntaría inmediatamente si no sería posible encontrar una ecuación capaz de representarlas analíticamente y, en segundo lugar, su interés se dirigiría hacia el origen de la radiación. Se intentó obtener tal ecuación, basándose en los postulados de la termodinámica y de la electrodinámica clásica. Los resultados fueron poco menos que un fracaso total y, finalmente, Max Planck, prescindiendo de algunos conceptos clásicos, postuló que la energía radiante no se emite de una manera continua, sino por cuantos. Una frecuencia determinada se emite en pequeñas porciones o cuantos, actualmente llamados fotones, que llevan consigo una energía proporcional a la frecuencia, f de la radiación. Así,
   
   
   Energía del fotón o cuanto = h x f
   
   
   en que h es la famosa constante de Planck, cuyo valor es igual a 6,55 x 10^(-27) ergios por segundo.
   
   
   El detalle de los razonamiento de Planck es demasiado complicado para traerlo a este lugar, pero la forma definitiva de su ecuación es:
   
   
   Eλ = 2π C²λ^(-5) (e^(hf/kτ) - 1)^(-1)
   
   
   en la que C es la velocidad de la luz; h, la constante de Planck; λ, la longitud de onda que se considera; τ, la temperatura absoluta y k la constante de Boltzmann o constante molecular de los gases. El término Eλ es la emisividad por unidad de longitud de onda. Las curvas experimentales concuerdan con esta ecuación con una notable precisión que disipa todas las dudas acerca de su validez, aunque pueda discutirse el procedimiento empleado por Planck para obtenerla. La idea de la emisión o radiación cuantizada era tan nueva para los contemporáneos de Planck, que muy probablemente no habría sido aceptada si Albert Einstein no la hubiera apoyado con su ley tan conocida del efecto fotoeléctrico.
   
   Heinrich Rudolf Hertz ya había descubierto en 1883 que podían obtenerse fuertes descargas entre electrodos a potencial elevado, cuando éstos se exponían a la acción de la luz. Una modificación posterior del experimento demostró que cuando la luz ultravioleta incide sobre una superficie como la del cinc, ésta se carga positivamente, como consecuencia de que un cierto número de electrones la han abandonado. Einstein afirmó que un fotón con suficiente energía puede, al incidir en la superficie, despedir un electrón con una energía cinética dada por la ecuación:
   
   
   1/2 mv² = hf- w
   
   
   en la que hf es la energía asociada a un fotón de frecuencia f y w es la función de trabajo del metal, es decir, la energía necesaria para separar un electrón de la superficie en que se encuentra. Una experimentación cuidadosa demostró que h tiene el mismo valor que obtuvo Planck en su estudio de la radiación del cuerpo negro. Esta comprobación dejó pocas dudas respecto a la validez de la hipótesis de los cuantos y amplió su alcance mucho más allá de lo logrado por Planck. Al explicar el efecto fotoeléctrico, Einstein cuantizó la radiación misma, mientras que Planck se había limitado a cuantizar el comportamiento de sus emisores u osciladores.
   
   Las teorías del mecanismo de la absorción del calor por los cuerpos y las de los calores específicos han sido poco satisfactorias. Las más corrientes suponen que en el caso de los sólidos, cada grado de libertad del átomo o de la molécula participa con los demás por igual en la absorción del calor. Por ejemplo, en el cinc, cuyos átomos se suponen en constante vibración, a cada grado de libertad corresponde una cantidad igual de energía cinética y potencial, de dos calorías por equivalente gramo. Como el cinc tiene en estado sólido tres grados de libertad, se obtiene un calor atómico de valor seis, aproximadamente. En la mayoría de los elementos sólidos el calor atómico es algo superior a seis (ley de Dulong y Petit). Sin embargo, conforme desciende la temperatura, disminuye el calor atómico, tendiendo hacia cero en el cero absoluto de temperatura. En la teoría de la equipartición de la energía no hay manera de encajar esta influencia de la temperatura sobre el calor específico. Einstein estudió el problema suponiendo una absorción cuantizada por parte de los átomos y llegó a una solución en completo acuerdo con los datos experimentales.
   
   Una inmediata aplicación de la teoría cuántica fue el estudio de las rayas de los espectros de emisión. Sir Emest Rutherford, después de realizar una serie de brillantes experiencias, llegó en 1911 a la conclusión de que el átomo de cualquier sustancia se compone de un núcleo cargado positivamente, en el que la materia se encuentra muy concentrada, al que se asocian un cierto número de electrones extranucleares. Antes de ello, los espectroscopistas habían logrado algunos progresos y encontrando relaciones matemáticas en las series espectrales de muchos elementos, pero no había ninguna teoría satisfactoria acerca del origen de la radiación. El danés Niels Bohr, de Copenhague, discípulo de Rutherford en el Laboratorio Cavendish de la Universidad de Cambridge, concibió en 1913 la idea de que los electrones giraban en una serie de órbitas circulares alrededor del núcleo del átomo de Rutherford.
   
   Para explicar el origen de los diferentes espectros del hidrógeno, formuló dos postulados:
   
   
   1) El electrón que gira en una órbita circular alrededor del núcleo debe tener un momento angular que sea múltiple de h/2π. Así:
   
   mvr = nh/2π
   
   
   donde m es la masa de un electrón que gira con una velocidad v en una órbita de radio r; n, es un número entero asociado a cada órbita y empieza con el valor unidad para la más interna y más estable. Como el momento está cuantizado, la energía de una órbita cualquiera queda perfectamente determinada.
   
   
   2) Cuando un electrón, por efecto de una colisión o de algún otro fenómeno, se ve obligado a girar en una órbita más alejada es porque ha adquirido una mayor energía y se encuentra en una situación inestable. Al volver a una órbita más cercana al núcleo y, por tanto, de menor energía, emite un cuanto o fotón de energía radiante. Así, si Ex es la energía correspondiente a la órbita exterior y Eg la de la interior:
   
   Ex - Eg = hf
   
   
   en la que h sigue siendo la constante de Planck y f es la frecuencia de la radiación emitida. Esta condición constituye el llamado principio de correspondencia de Bohr. La aplicación de las dos condiciones antes dichas al comportamiento del electrón que gira alrededor del núcleo del átomo del hidrógeno permitió establecer unas ecuaciones, a base de las cuales pueden calcularse las longitudes de onda de varios espectros de emisión, como los del hidrógeno y del helio ionizado, con una precisión muy notable, aunque el problema sigue en pie por lo que respecta a los átomos de estructura más complicada. Por otra parte, esta teoría dio también un tremendo impulso al posterior desarrollo de la espectroscopia.
   
   Unos diez años más tarde, Louis de Broglie lanzó la idea de que si el comportamiento de la luz es tan parecido al de las ondas como al de las partículas, la materia debe también participar de esta doble naturaleza, es decir, que los electrones y los protones han de poder actuar como partículas, pero también como ondas. Esta nueva concepción física fue desarrollada rápidamente por los dos físicos alemanes Heisenberg y Schroedinger.
   
   La primera confirmación experimental de esta teoría se debe a Davisson y Germer, de los Bell Telephone Laboratories de Nueva York, quienes en 1927 se dedicaban a estudiar la naturaleza de superficies cristalinas como la calcita mediante las imágenes producidas por los haces electrónicos reflejados por ellas, que resultaban muy semejantes a las obtenidas con los rayos X en las mismas condiciones. Conociendo la velocidad de los electrones utilizados y los ángulos bajo los cuales se reflejan con mayor intensidad, y mediante la ecuación de De Broglie, λ = h/mv (en la que λ es la longitud de onda asociada a una partícula de masa m, que se mueve con una velocidad vf y h la constante de Planck) pudieron calcular la longitud de onda correspondiente a dichos electrones.
   

   ---

   
   
   
   Mecánica ondulatoria.
   
   
   La teoría de los cuantos, ampliada y generalizada posteriormente, ha pasado a constituir en la actualidad la llamada mecánica cuántica u ondulatoria, de la que aquí sólo puede darse una ligera idea, de carácter muy general.
   
   Como se supone que los electrones son ondas que se encuentran distribuidas en el espacio en lugar de concentrarse en algún punto de una órbita de Bohr, la teoría orbital ha sido desplazada por la idea de que en el espacio, alrededor del núcleo, existen en todo momento regiones en las que es más probable que se encuentren los electrones. Sin embargo, el concepto de los estados o niveles energéticos de la teoría de Bohr continúa conservando su validez en la mecánica ondulatoria, de mucho mayor alcance que aquélla, ya que es capaz de asignar niveles energéticos a los átomos más complicados, problema que había dejado sin resolver la teoría de Bohr.
   
   Para hacerse una idea de cómo se llega al primer postulado de Bohr en la mecánica ondulatoria, basta considerar al electrón como un tren de ondas circular, alrededor del núcleo, compuesto por un número entero de longitudes de onda, n = 2πr/λ. Como en la mecánica ondulatoria la longitud de onda asociada al electrón es λ = h/mv, combinando ambas igualdades resulta mvr = nh / 2π, que es precisamente la expresión de dicho postulado.
   
   La mecánica ondulatoria se ha desarrollado hasta el punto de que hoy constituye una sólida base para la física atómica y nuclear. Por desgracia, sus ecuaciones diferenciales no resultan tan atractivas para el hombre medio como el sencillo modelo atómico de Bohr. Véase Átomo; Calor atómico; Teoría atómica.

Compartir

Buscar

Asistente IA

Consulta nuestro asistente de Inteligencia Artificial
¡te responderá en segundos!

Respuesta completa
Respuesta corta

[ Ayuda ] Dale información suficiente de lo que buscas, dale un contexto. El Asistente te puede dar definiciones, sinónimos y antónimos, oraciones de uso de palabras, encontrar ideas relacionadas, corregir ortografía y darte asistencia escolar sobre cualquier tema. Igualmente, te recomiendo FUERTEMENTE que uses nuestro Buscador (más abajo) para encontrar información apropiada, ya que esta fue escrita por nuestros expertos.

* ACLARACIÓN: sugerimos dejar un email para que te contactemos si vemos errores en la respuesta de la IA: leemos todas las consultas.

Esta imagen puedes emplearla con fines didácticos en la escuela, institución educativa o proyectos web.

¿Hay un error o desea enviarnos un mensaje?: enviar mensaje

No hay ningún comentario todavía